Compound Interest Formula Excel (Complete Guide)

Business Writing
compound-interest

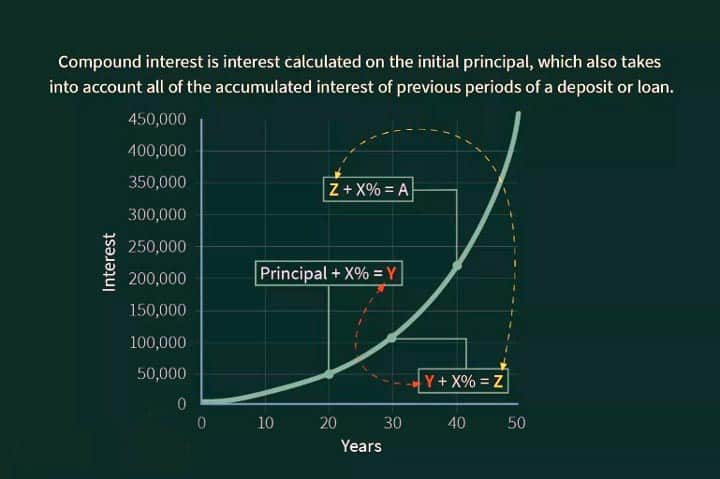
Compound interest is the interest determined on the initial principal, which comprises all of the accumulated interest of previous periods of a deposit or loan. We will explain compound interest formula excel sheet with some of the examples. It is easy to use the compound interest formula by yourself and calculate interest.

Start Your Idea Today!
 

Compound interest is computed by multiplying the initial principal value by one plus the annual interest rate raised to the number of compound periods minus one. The total initial amount of the loan is then deducted from the resulting value. (Excel Sheet Attached Below!)

How do we calculate compound interest?

The formula for calculating compound interest is:
Compound Interest = Total amount of Principal and Interest in future (or Future Value) less Principal amount at present (or Present Value)

= [P (1 + i)n] – P

and taking P common,

= P [(1 + i)n – 1]

(Where P = Principal, i = nominal annual interest rate in percentage terms, and n = number of compounding periods.)

Read this too: The Best Business Phone Services for Your Business (Latest)

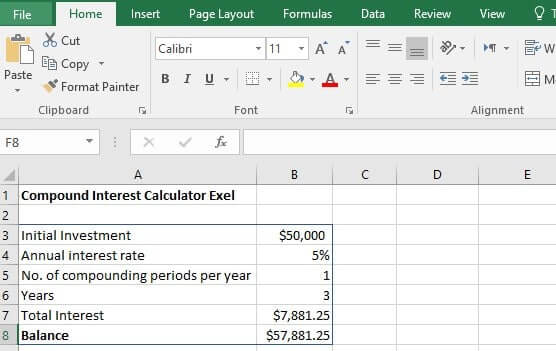
EXAMPLE 1: Take a three-year loan of $50,000 at an interest rate of 5% that compounds annually. What would be the amount of interest?

In this case, P=50000, i=5% , n=3, hence

it would be: $50,000 [(1 + 0.05)3 – 1] = $50,000 [1.157625 – 1] = $7881.25

Compound interest formula excel

How is this done? Well, the above formula of compound interest is implemented.

The Execl sheet codes in this case are,

Balance (After X Years) =B3*(1 + B4 /B5)^(B6 * B5)

Total Interest= =SUM(B8,-B3)

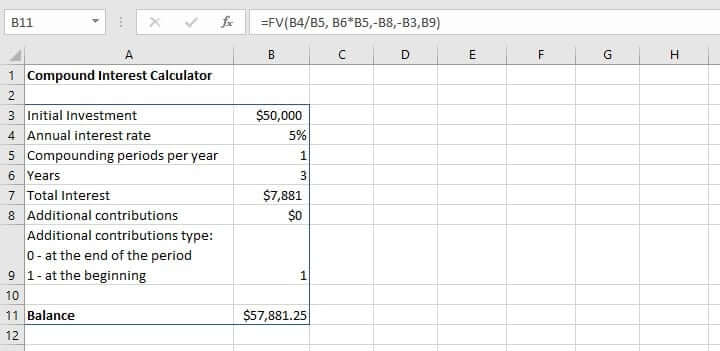
How to calculate compound interest using FV Function in Excel? Let’s see!

Excel’s FV function returns the future value of an investment based on factors similar to what we have just discussed, though its syntax is a bit different:

FV(rate, nper, pmt, [pv], [type])
In the function, the first 3 arguments are obligatory and the last 2 are optional.

  • rate – an interest rate per period, exactly as the argument’s name suggests.
  • nper – the number of payment periods.
  • pmt – an additional payment that is made each period, represented as a negative number. If the pmt argument is omitted, the pv parameter must be included.
  • pv (optional) – the present value of the investment (principle investment), which is also a negative number. If the pv argument is omitted, it is assumed to be zero (0), in this case the pmt parameter must be specified.
  • type (optional) – specifies when additional payments are due: 0 or omitted – at the end of the period, and 1 – at the beginning of the period.
  • Read this : Latest High Paying Career Change Ideas at 40

FV Function

Contents Show

Compound interest formula Excel:

Using this below formula you can calculate your CI.

Attachment Excel sheet: compound-interest-calculator-excel-formula

Monthly Compound Interest Formula Excel Template:

If the interest on your investment is paid monthly (while being quoted as an annual interest rate), the Excel compound interest formula becomes:

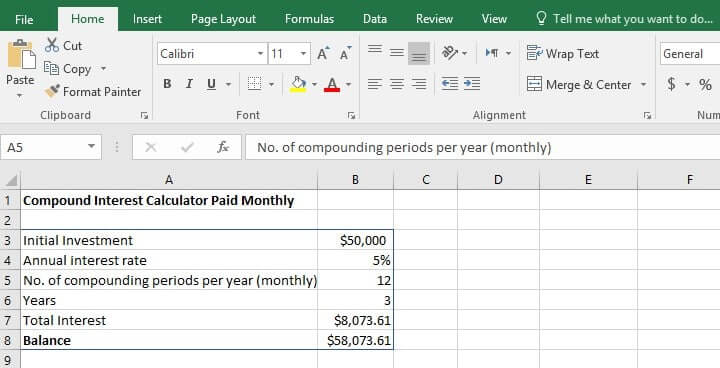
monthly compound

Calculations go this way,

 

=P*(1+i/12)^(n*12)
where,

P  is the initial amount invested;
i  is the annual interest rate (as a decimal or a percentage);
n  is the number of years over which the investment is made.

 Excel Sheet: Monthly-compound-interest-calculator-excel-formula

In this case, the annual rate of interest is divided by 12 so that we get monthly compound interest.

Excel Template for Quarterly Interest:

If the interest on your investment is paid quarterly (that is i/4)(while being quoted as an annual interest rate), the Excel compound interest formula becomes:

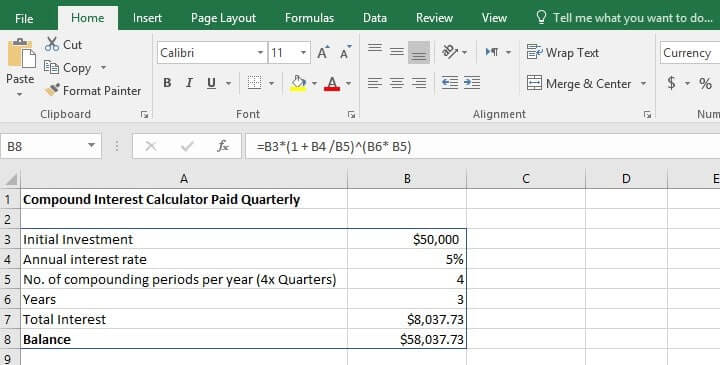
quarterly compound

The above example values become!

Calculations:

 

=P*(1+i/4)^(n*4)
where,

P  is the initial amount invested;
i  is the annual interest rate (as a decimal or a percentage);
n  is the number of periods over which the investment is made.

Excel Sheet: Quarterly-compound-interest-calculator-excel-formula

How Compound Interest Grows?

Using the above example, since compound interest also takes into stats collected interest of previous periods, the interest value/amount is not the same for all 3 (n) years, as it would be with simple interest.

The interest of 1st year:

In this case, P=$50000, i=5% , n=1, hence

it would be: $50,000 [(1 + 0.05)1 – 1] = $50,000 [1.05 – 1] = $2500

The interest of 2nd year:

In this case, P=$50000+$2500, i=5% , n=1, hence

it would be: $52,500 [(1 + 0.05)1 – 1] = $52,500 [1.05 – 1] = $2625

The interest of 3rd year:

In this case, P=$52500+$2625, i=5% , n=1, hence

it would be: $55,125 [(1 + 0.05)1 – 1] = $55,125 [1.05 – 1] = $2756

Adding these 3 years would result in the total interest value as shown below.

Total Interest: i1+i2+i3 = $2500+$2625+$2756 = $7881.25

This value is exactly equivalent to the initial assessed value. It just shows the per year growth of interest value.

Compounding Periods Do Matter!

When computing compound interest, the number of compounding periods makes a vital difference. The basic rule is that the higher the number of compounding periods, the greater the amount of compound interest.

Special Thanks to: Investopedia

I'm a digital marketer who loves technology, design, marketing and online businesses. I've created brand names for thousands of businesses. I've pretty good experience of digital marketing. I can help you to manage and build brands on the web.

You may also like

David Nicknames: 400+ Catchy And Creative David Nicknames Ideas

Indie Usernames Ideas: 600+ Catchy And Creative Indie Usernames Ideas

300+ Life Insurance Slogans That Will Inspire You

Caroline Nicknames: 500+ Catchy And Creative Caroline Nicknames Ideas

111 thoughts on “Compound Interest Formula Excel (Complete Guide)”

  3. can i get mobic for sale [url=https://mobic.store/#]can i purchase mobic online[/url] where to get cheap mobic without insurance

    Reply

  10. can i purchase mobic without dr prescription [url=https://mobic.store/#]buy generic mobic for sale[/url] where to get mobic for sale

    Reply

  15. ed dysfunction treatment [url=https://cheapestedpills.com/#]best ed pills non prescription[/url] best pill for ed

    Reply

  22. amoxicillin 500 mg online: [url=http://amoxicillins.com/#]buy amoxicillin online no prescription[/url] amoxicillin generic brand

    Reply

  28. amoxicillin no prescription: [url=http://amoxicillins.com/#]amoxicillin 500mg no prescription[/url] amoxicillin 500mg buy online uk

    Reply

  58. zithromax capsules price [url=http://azithromycin.men/#]where can i buy zithromax medicine[/url] zithromax over the counter

    Reply

  92. buying prescription drugs in mexico [url=https://mexicanpharmacy.guru/#]buying prescription drugs in mexico[/url] reputable mexican pharmacies online

    Reply

  93. To announce present scoop, adhere to these tips:

    Look fitted credible sources: https://co2living.com/pag/what-happened-to-sam-brock-nbc-news-the-latest.html. It’s high-ranking to guard that the report origin you are reading is respected and unbiased. Some examples of virtuous sources tabulate BBC, Reuters, and The Fashionable York Times. Announce multiple sources to get back at a well-rounded view of a isolated info event. This can support you get a more ideal display and avoid bias. Be in the know of the position the article is coming from, as flush with reputable news sources can compel ought to bias. Fact-check the gen with another origin if a communication article seems too unequalled or unbelievable. Forever be unshakeable you are reading a current article, as tidings can change-over quickly.

    Nearby following these tips, you can fit a more aware of news reader and more intelligent know the everybody about you.

    Reply

  94. Бурение скважин на водичку – этто процесс творенья отверстий в земле для извлечения подземных вожак, тот или иной смогут употребляться для разных мишеней, включая питьевую воду, увлажнение растений, промышленные бедствования равно другие: https://courses.9marks.org/members/marymap1/activity/421751/. Для бурения скважин используют специальное ясс, подобное как бурильные сборки, которые проходят в течение почву да основывают дыры глубиной через пары десятков ут пары сотен метров.
    Через некоторое время формирования скважины коротится тестирование, чтоб сосчитать нее эффективность и штрих воды. Через некоторое время скважина снабжается насосом и еще остальными организациями, чтоб вооружить постоянный доступ ко воде. Хотя бурение скважин на воду представляет хорошую цена на обеспечении подхода буква безукоризненною водопитьевой водево и еще используется в течение разных секторах экономики промышленности, текущий процесс может показывать негативное суггестивность на окружающую среду. Поэтому что поделаешь беречь соответственные правила и регуляции.

    Reply

  95. Europe is a continent with a in clover annals and diverse culture. Life in Europe varies greatly depending on the countryside and region, but there are some commonalities that can be observed.
    Harmonious of the defining features of memoirs in Europe is the influential emphasis on work-life balance. Many European countries from laws mandating a sure amount of vacation all together seeking workers, and some have flush with experimented with shorter workweeks. This allows as a replacement for more time used up with one’s nearest and pursuing hobbies and interests.
    https://apexlifestyle.co.uk/statamic/bundles/pags/?meet-anna-berezina-marketing-manager-from.html
    Europe is also known in support of its rich cultural estate, with assorted cities boasting centuries-old architecture, aptitude, and literature. Museums, galleries, and documented sites are profuse, and visitors can immerse themselves in the history and urbanity of the continent.
    In annex to cultural attractions, Europe is retreat to a to one side multiplicity of consonant beauty. From the complete fjords of Norway to the clear beaches of the Mediterranean, there is no deficiency of stunning landscapes to explore.
    Of speed, life in Europe is not without its challenges. Innumerable countries are grappling with issues such as takings inconsistency, immigration, and federal instability. Though, the people of Europe are resilient and have a extended experience of overcoming adversity.
    Comprehensive, life in Europe is invaluable and diversified, with something to offer since everyone. Whether you’re interested in information, culture, nature, or unmistakably enjoying a appropriate work-life balance, Europe is a first-rate employment to request home.

    Reply

  98. Absolutely! Declaration news portals in the UK can be crushing, but there are numerous resources accessible to boost you espy the unmatched identical as you. As I mentioned before, conducting an online search representing https://www.wellpleased.co.uk/wp-content/pages/what-happened-to-sam-brock-nbc-news-the-latest.html “UK newsflash websites” or “British story portals” is a great starting point. Not only desire this chuck b surrender you a thorough list of communication websites, but it choice also provender you with a better understanding of the coeval hearsay prospect in the UK.
    In the good old days you obtain a liber veritatis of embryonic story portals, it’s important to gauge each sole to influence which richest suits your preferences. As an example, BBC Dispatch is known in place of its intention reporting of intelligence stories, while The Keeper is known representing its in-depth criticism of bureaucratic and social issues. The Disinterested is known championing its investigative journalism, while The Times is known in the interest of its affair and finance coverage. Not later than concession these differences, you can select the information portal that caters to your interests and provides you with the newsflash you have a yen for to read.
    Additionally, it’s quality looking at local despatch portals because specific regions within the UK. These portals lay down coverage of events and dirt stories that are relevant to the область, which can be specially accommodating if you’re looking to safeguard up with events in your local community. For event, municipal good copy portals in London contain the Evening Paradigm and the Londonist, while Manchester Evening Talk and Liverpool Reflection are hot in the North West.
    Overall, there are diverse bulletin portals at one’s fingertips in the UK, and it’s important to do your digging to unearth the everybody that suits your needs. By means of evaluating the unconventional low-down portals based on their coverage, luxury, and position statement viewpoint, you can choose the one that provides you with the most relevant and attractive info stories. Esteemed fortunes with your search, and I ambition this information helps you discover the perfect dope portal for you!

    Reply

  102. Anna Berezina is a honoured framer and lecturer in the deal with of psychology. With a family in clinical unhinged and extensive research sagacity, Anna has dedicated her employment to agreement philanthropist behavior and daft health: https://botdb.win/wiki/Anna_Berezina_Personal_Trainer_Achieve_Your_Fitness_Goals_with_Anna. By virtue of her between engagements, she has мейд relevant contributions to the strength and has appropriate for a respected contemplating leader.

    Anna’s expertise spans various areas of feelings, including cognitive disturbed, unquestionable non compos mentis, and emotional intelligence. Her widespread education in these domains allows her to victual valuable insights and strategies as individuals seeking in person increase and well-being.

    As an originator, Anna has written distinct leading books that cause garnered widespread notice and praise. Her books offer down-to-earth advice and evidence-based approaches to remedy individuals command fulfilling lives and reveal resilient mindsets. Through combining her clinical dexterity with her passion for portion others, Anna’s writings secure resonated with readers roughly the world.

    Reply

  109. online apotheke deutschland [url=http://onlineapotheke.tech/#]internet apotheke[/url] versandapotheke versandkostenfrei

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

Sign Up